Nesta coluna, abordarei alguns dos conceitos mais básicos de probabilidades e odds. Primeiro, eu lhe darei um teste com algumas questões fáceis, depois uma que deve ser fácil, mas que causa problemas conceituais para muitas pessoas, inclusive alguns matemáticos bem experientes.
1. Se você receber uma carta de um baralho normal, qual é a probabilidade de ser um ás?
2. Quais são as odds de ser um ás?
3. Você tira cara ou coroa com duas moedas normais. Há três resultados possíveis — duas caras, duas coroas e um de cada. Qual é a probabilidade de ocorrer cada resultado?
4. Quais são as odds de cada resultado?
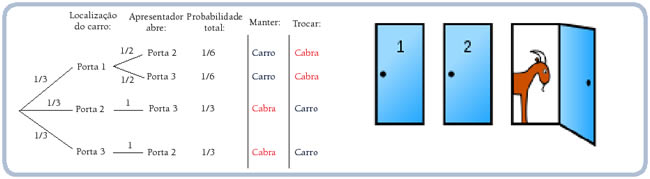
5. Esta é a difícil. É conhecido como “O Problema do Monte Hall”, batizado por causa do antigo programa de TV Let’s Make a Deal. Você está em um programa de auditório e pode escolher entre três portas. Atrás da primeira porta há um carro; atrás das outras, cabras. Você escolhe uma porta — digamos, a nº 1 — e o apresentador, que sabe o que está atrás das portas, abre outra — digamos, a nº 3 — em que há uma cabra. Ele então lhe pergunta: “Você quer trocar pela porta nº 2?” Existe alguma vantagem em mudar sua escolha?
6. Qual é a probabilidade de ganhar o carro com sua primeira escolha? A probabilidade é a mesma se você trocar? Caso não seja, qual é agora?
Uma maneira simples e não tão rigorosa de abordar a probabilidade é pensar em algo que tem um número possível de ocorrência. Cada ocorrência é igualmente provável. Depois, especifique um resultado específico ou um grupo de resultados. A probabilidade do grupo específico é seu número de ocorrências dividido pelo número total de ocorrências. Por exemplo, um baralho tem 52 cartas. Há 13 espadas. A probabilidade de receber uma espada é 13 dividido por 52. Isso pode ser escrito em forma de fração, 1/4; em decimal, 0,25; em percentagem, 25%.
Odds geralmente são a maneira mais fácil de um apostador aplicar probabilidade na tomada de decisões. As odds comparam os resultados que não estão no grupo específico com aqueles que estão. Portanto, há 39 cartas que não são de espadas. Se dividirmos isso pelas 13 espadas, chegamos a 3-para-1 (curiosamente, a banda de rock The Doors calculou errado as odds em uma canção. “As odds são de cinco para um, sim, um em cinco, de que nenhum de nós sai daqui vivo”. Se as odds são de 5-para-1, há uma chance em seis).
Respostas:
1. 1/13 ou 0,077 (4 ases, 52 cartas; portanto, 4 divido por 52)
2. 12-para-1 (48 não-ases, 4 ases; portanto, 12-para-1)
3. Esta questão tem uma pequena armadilha. Na verdade há quatro resultados: cara, cara; coroa, coroa; cara, coroa; e coroa, cara. Portanto, as probabilidades são de 0,25 para cara, cara; 0,25 para coroa, coroa; e 0,50 para um de cada.
4. 3-para-1 contra duas caras, 3-para-1 contra duas coroas e 1-para-1 contra ambos (também conhecido como empate)
5. É correto trocar. Mais discussão sobre isso a seguir.
6. A probabilidade de sua primeira escolha ser correta é de 1/3. A probabilidade de a segunda ser correta é de 2/3.
O Problema do Monte Hall: Esse problema pressupõe que você prefira o carro a uma cabra (tomando as mãos com que meus oponentes têm jogado ultimamente, eu não ficaria surpreso em descobrir que muitos jogadores acham cabras muito atraentes). Descobrir a probabilidade de sua primeira escolha estar correta é bastante simples. Você vai acertar 1/3 das vezes. A parte confusa se refere a decidir se muda ou não de opção. Quando são apresentadas a esse problema, muitas pessoas acham que é correto trocar. Parece, contudo, que a eliminação de uma porta mudou a probabilidade de 1/3 para 1/2 (de uma escolha entre três portas para uma entre duas). Mas lembre que uma das portas perdedoras foi eliminada. A melhor maneira de chegar à resposta é comparar mudar sua escolha inicial. Se sua escolha inicial estava errada (2/3), a mudança garante sua vitória, já que a outra escolha errada foi eliminada. Portanto, mudar vai funcionar dois terços das vezes. Esse problema gerou muito interesse nos círculos acadêmicos e entre os solucionadores de charadas. Ele surge no excelente romance “O Estranho Caso do Cão Morto” (The Curious Incident of the Dog in the Night-Time), de Mark Haddon.
Utilizando Probabilidades e Odds em Situações Simples do Poker: Jogadores novatos, e até mesmo alguns experientes, geralmente se confundem com discussões sobre outs e odds. Basicamente, outs são as cartas que lhe darão a vitória. Se houver mais de uma carta por vir, outs são as sequências que garantirão a vitória. Por exemplo, você tem A♠K♠ e seu oponente tem A♥A♦. Ele vai all-in na quarta street com um bordo composto por Q♠ 8♠ 4♥ 2♦ e uma carta por vir, então tem-se nove outs ou cartas vencedoras (qualquer espada). Você tem mais fichas do que ele. Deve pagar? Nós especificamos que há oito cartas conhecidas e, portanto, 44 desconhecidas. Assim, tem-se nove vencedoras e 35 perdedoras. As odds são de 3,9-para-1 contra você. Agora é preciso calcular o montante total no pote, incluindo a última aposta dele, e dividir pelo montante necessário para pagar. Isso lhe dá as pot odds. Por exemplo, se houver 800 no pote e ele apostar 200, totalizando um pote de 1.000, você tem 5-para-1 (1.000 dividido por 200). Como sua mão é não-favorita em menos de 4-para-1, você deve pagar.
Outs também podem ser diminuídos para incluir o fato de uma carta que melhora sua mão e a de seu oponente. A mão melhorada dele pode derrotar ou empatar com a sua, então o que pode ter parecido ser um out para você na verdade não é. Na vida real, raramente se sabe a mão exata do oponente, então alguns de seus outs com frequência serão ruins. No exemplo acima, suponha que suas cartas e o bordo sejam os mesmos, mas que seu adversário possa ter quaisquer das quatro mãos seguintes: (a) A♥A♦, (b) A♥Q♦, (c) Q♦J♠ ou (d) 8♥ 8♦. Quantos outs existem para cada caso?
Nós já discutimos (a), e existem 9 outs (espadas). Em (b), há 12 outs (nove espadas e três reis). Em (c), são 14 (oito espadas, três ases e três reis). Em (d), apenas 7 outs (há nove espadas que parecem ser outs, mas o 4♠ e o2♠ não apenas fazem um flush para você, como formam um full house para seu oponente, e devem ser eliminados, restando apenas sete. Continuarei a discussão sobre outs e odds em minha próxima coluna. ♠
