Nota do editor: o que se segue é uma prévia especial do próximo livro de Jeff Hwang, Pot-Limit Omaha Poker: Advanced Play Vol. I, previsto para ser lançado pela Dimat Enterprises no primeiro semestre de 2009.
Na última edição, nós analisamos equidade de draw, que definimos como nossa parcela do pote derivada do valor tangível da mão — como um flush ou straight draw, ou mesmo um draw para dois pares ou uma trinca em alguns casos. Conforme notamos, equidade de draw deriva-se de uma com-binação entre equidade direta e implícita.
Ao contrário, equidade de float é nosso valor intangível derivado de uma combinação de equidade de fold e o valor da informação que nosso oponente nos dá quando pede mesa com intenção de desistir de uma aposta. Não é importante (ou exequível) ser capaz de calcular a equidade de float na mesa, mas é importante ser capaz de conceituá-la. Dito isso, eis as duas informações básicas que você precisa saber sobre equidade de float:
1. A equidade de float tem valor real — às vezes considerável — que pode potencialmente tornar lucrativo dar call com valores de mão que de outro modo seriam pequenos.
2. O valor da equidade de float depende muito de nossos oponentes.
Afirmativa nº 1: A equidade de float tem valor real
Voltando ao exemplo de nossa discussão sobre equidade de draw na edição passada, estávamos heads-up em posição depois do flop, havia $100 no pote, e nós tínhamos um estoque de $2.000. Segurávamos A♠K♠Q♦3♣, e o flop veio 8♠7♣2♠. Mais uma vez, nosso oponente aposta $100. Dessa vez, ele vai pedir mesa e desistir sempre que uma carta de espadas aparecer no turn (nove cartas). Mas além disso, nosso observador oponente percebe um valete ou um 6 e completa uma potencial queda para duas pontas (ficando nuts), e também vai pedir mesa ou desistir diante de uma aposta do tamanho do pote 100% das vezes em que um valete ou um 6 surgir, o que nos dá seis outs de float.
O resultado é que nosso oponente vai pedir mesa e desistir diante de 15 de 45 cartas possíveis — ou 33% das cartas que aparecerem no turn. Agora, nesse caso, nós não temos nenhuma equidade implícita porque nosso oponente desiste quando acertamos o flush,mas efetivamente temos 33% da equidade de pote de que precisamos para justificar pagar uma aposta do tamanho do pote em razão dos seis outs de float.
Nut-Flush Draw Mais Seis Outs de Float, Nenhum Valor Implícito
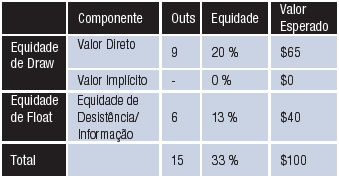
E se dermos raise diante de 100% dos pedido de mesa seguido de fold de nosso inteligente oponente para incluir qualquer carta de straight que complete o nut wrap de 13 cartas (J-10-9-X em um bordo de 8-7-2), ele também vai pedir mesa e legar se um 10 ou 9 aparecerem no turn, o que dá mais seis outs de float, totalizando 12. Agora ele vai pedir mesa e desistir diante de 21 de 45 cartas, ou quase 47% das vezes. Agora, de repente, temos $140 de valor esperado em nosso call de $100, com um lucro de $40, e a equidade de float tornou bastante lucrativo pagar com apenas o nut-flush draw contra nosso solitário oponente.
Nut-Flush Draw Mais 12 Outs de Float, Nenhum Valor Implícito
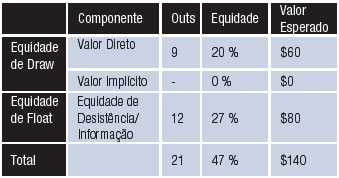
Afirmativa nº 2: Equidade de float depende muito do jogador
O valor da equidade de float é altamente dependente do jogador, e às vezes de maneira desenfreada. Isso ocorre porque o float depende da informação recebida quando nosso oponente pede mesa no turn. O problema é que dois jogadores com a mesma mão podem reagir de forma diferente diante das mesmas cartas perigosas.
Digamos que ainda estejamos heads-up em posição depois do flop, com $100 no pote e um estoque de $2.000. Mais uma vez, temos A♠K♠Q♦3♣, e o flop vem 8♠ 7♣ 2♠. Contudo, dessa vez nosso oponente tem especificamente A♦A♥K♦K♥. Ele aposta $100 no flop e nós pagamos.
Agora vamos imaginar nosso oponente como sendo o jogador mais fraco do mundo, e dizer que ele vai pedir mesa e desistir diante de qualquer carta do turn, com exceção de A♣ or K♣, as duas cartas que dão a ele o nuts. Nesse caso, nós efetivamente temos 95% de equidade para pagar, pois nosso oponente agora vai pedir mesa e largar diante de 39 de 41 cartas. Nove outs são atribuíveis ao flush draw, totalizando 22% (9÷4) de equidade direta, enquanto os outros 30 outs são atribuíveis ao float, o que nos dá 73% (30÷41) de equidade de float a nosso call.
Embora esse possa parecer um caso muito extremo, ele na verdade não está muito longe da realidade como parece, pois muitos jogadores — e não apenas os extremamente fracos — que seguram A♦A♥K♦K♥, com um único par, dariam fold se não melhorassem no turn, com medo de estarem atrás de alguém com uma trinca ou dois pares. Sob a perspectiva deles, eles já estão atrás ou não muito à frente de um draw.
Quer dizer, se você estivesse segurando A♦A♥K♦K♥, e apostasse no pote e alguém pagasse num flop com 8♠7♣2♠, até onde você iria com essa mão? Dito isso, muitos jogadores prefeririam desistir de um pote pequeno do que arriscar perder um grande pote com apenas um par.
Contra o Oponente Mais Fraco Com A♦ A♥ K♦ K♥:
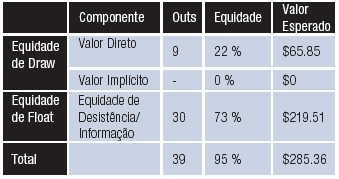
Ele Pede Mesa e Desiste no Turn 95% das Vezes
Contudo, alguns jogadores não apostam apenas quando têm força: eles também continuam a apostar quando estão fracos.
Digamos que nosso oponente esteja do outro lado do espectro. Se ele for um maníaco que sempre aposta no pote no turn, nós teremos ganhado um valor implícito sobre nosso draw, mas perdido equidade de float porque não saberemos quando ele vai estar fraco desde o começo. Uma carta para a sequência, como o 10♦ ou o 9♥, podem criar equidade de fold — nosso oponente com A-A-K-K provavelmente desistiria diante de um aumento — mas essa equidade de fold não tem utilidade a não ser que nosso oponente nos diga que está fraco pedindo mesa (ou dando um golpe leve).
Nessa disputa, nós novamente vamos ter 22% de equidade direta em nosso call de $100 no flop, mas também teremos mais 22% de equidade implícita. Isso é bem fácil de descobrir, pois vamos acertar o flush e recuperar $300 do pote 22% das vezes, totalizando um valor esperado de $65,85, e vamos conseguir $300 adicionais de nosso oponente ao mesmo tempo, totalizando um EV dos mesmos $65,85, o que corresponde a 22% de equidade implícita.
O resultado é equidade de draw de 44% e EV de $131,70 ($31,70 de lucro em nosso investimento de $100 no flop). Mas, nesse caso, também temos zero de equidade de float, pois nosso oponente jamais pede mesa quando está fraco. Como tal, a equidade de draw compreende a equidade total contra esse oponente.
Contra o Maníaco Com A♦ A♥ K♦ K♥ Que Sempre Aposta no Turn
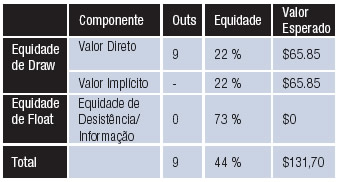
A conclusão é que, quanto mais fracos forem nossos oponentes, mais valioso o float se torna, e maior é nossa equidade de float. Ao contrário, quanto mais fortes ou simplesmente mais agressivos forem nossos oponentes, menos valioso o float se torna dentro e fora de si mesmo, e mais dependente nosso call fica do valor real da mão. ♠
Jeff Hwang é um jogador semiprofissional e autor de Pot-Limit Omaha Poker: The Big Play Strategy. Ele é também colaborador de longa data do Motley Fool. Você pode checar o website dele em www.jeffhwang.com



